Chapter 7 普通线性模型 - 回归第二部分

在本次研讨会中，我们将探讨一般线性模型 (GLM) 背景下的多元回归。多重回归建立在简单回归的基础上，不同之处在于，只有一个预测变量（就像简单回归的情况），我们将处理多个预测变量。同样，您将有机会构建一些回归模型并使用各种方法来决定哪一个是“最好的”。您还将学习如何对这些模型运行模型诊断，就像在简单回归中所做的那样。

概述

首先，我想让您观看以下视频，该视频是第一个回归工作坊的延续。我们将探讨如何使用R中的lm()函数构建具有多个预测变量的回归模型，测试我们的模型假设，并解释输出结果。我们将研究使用多个预测变量构建逐步回归模型的不同方法，最后讨论中介和调节。

多元回归

在标准多元回归中，所有自变量（independent variables, IVs）都被输入到方程中，并同时进行评估其贡献。让我们通过一个具体的例子来进行讲解。

教育心理学家进行了一项研究，调查了7至9岁的小学生的拼写能力与心理语言学变量之间的关系。研究人员向孩子们展示了48个单词，这些单词根据一定的特征进行了系统变化，如掌握年龄、词频、词长和形象性。心理学家想要检查测试结果是否准确反映了孩子们的拼写能力，这是通过标准化拼写测试来估计的。也就是说，心理学家想要检查她的测试是否合适。

儿童的实际年龄（以月为单位）（年龄），他们的阅读年龄（reading age, RA），他们的标准化阅读年龄（standardised reading age, std_RA）以及他们的标准化拼写分数（standardised spelling score, std_SPELL）被选择为预测变量。准则变量（Y）是每个孩子使用48个单词列表时达到的正确拼写百分比（percentage correct spelling, corr_spell）得分。

首先，我们需要加载我们需要的软件包 - require函数假设它们已经在您的计算机上。如果它们不在，那么您首先需要install.packages (“packagename”) ：

我们需要的包

library(tidyverse) # Load the tidyverse packages
library(Hmisc) # Needed for correlation
library(MASS) # Needed for maths functions
library(car) # Needed for VIF calculation
library(olsrr) # Needed for stepwise regression 
library(performance) # Needed to check model assumptions

导入数据

现在您需要读取数据文件。数据文件可以点击这里下载。

MRes_tut2 <- read_csv("Dataset/MRes_tut2.csv")

检查可能的关系

在我们开始之前，让我们来看一下我们的自变量IVs（预测因子，predictors）和因变量DV（结果，outcome）之间的关系。我们可以绘制图表来描述它们之间的相关性。我们将依次绘制测试表现与我们的四个预测因子之间的关系图：

ggplot(MRes_tut2, aes(x = age, y = corr_spell)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal() +
  theme(text = element_text(size = 13))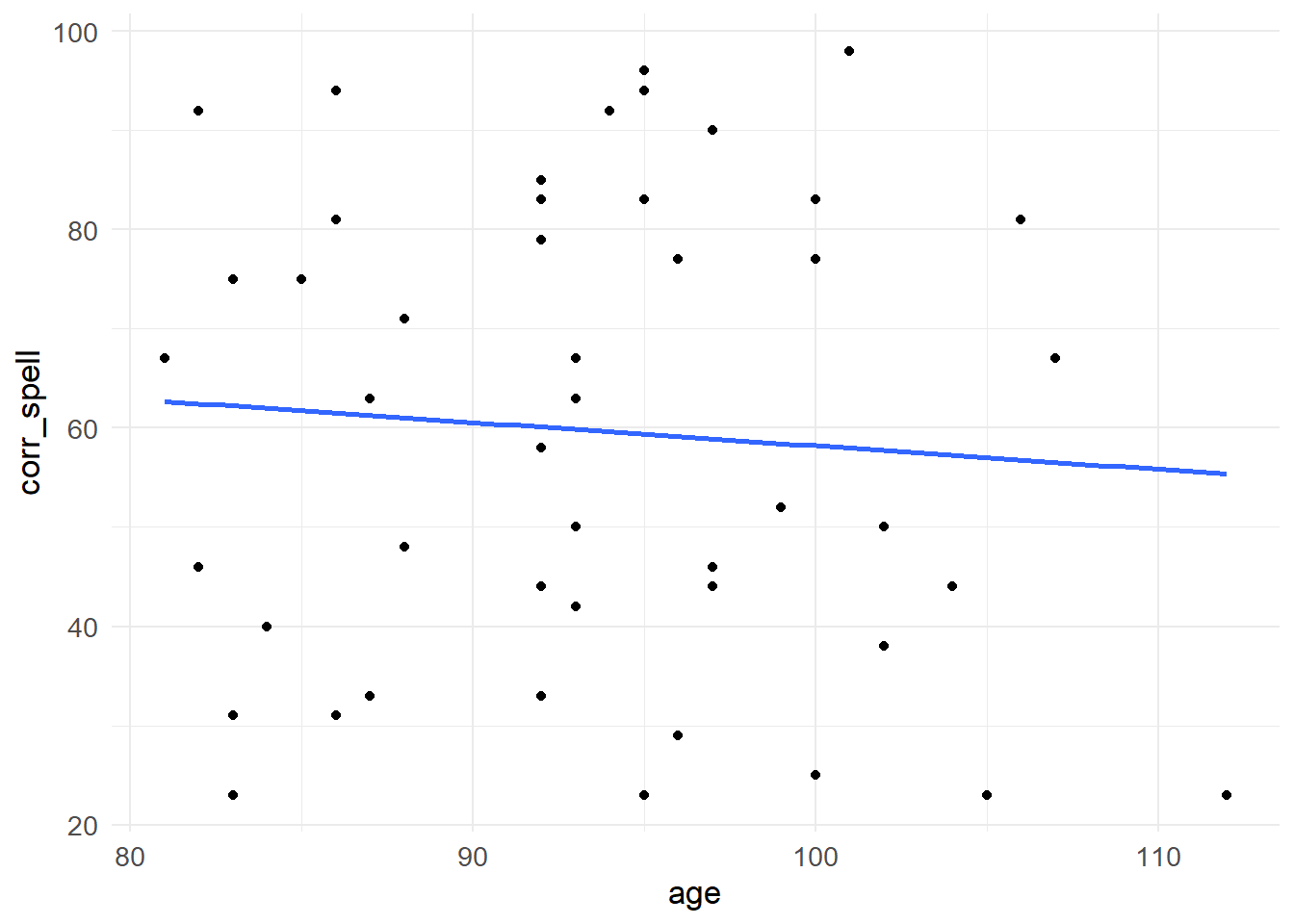

ggplot(MRes_tut2, aes(x = RA, y = corr_spell)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal() +
  theme(text = element_text(size = 13))

ggplot(MRes_tut2, aes(x = std_RA, y = corr_spell)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal() +
  theme(text = element_text(size = 13))

ggplot(MRes_tut2, aes(x = std_SPELL, y = corr_spell)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal() +
  theme(text = element_text(size = 13))

对数据建模

我们首先将进行分层回归 - 我们将构建一个模型（我们将其称为model0），该模型是我们结果变量的平均值，另一个模型（model1）包含所有的预测变量：

model0 <- lm(corr_spell ~ 1, data = MRes_tut2)
model1 <- lm(corr_spell ~ age + RA + std_RA + std_SPELL, data = MRes_tut2)

让我们将它们相互比较：

anova(model0, model1)

## Analysis of Variance Table
## 
## Model 1: corr_spell ~ 1
## Model 2: corr_spell ~ age + RA + std_RA + std_SPELL
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1     46 26348.4                                  
## 2     42  3901.1  4     22447 60.417 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

我们看到这些模型彼此不同（查看比较的p值），并且具有四个预测变量的模型具有较低的残差（RSS）值，这意味着模型与观测数据之间的误差相对于较简单的仅有截距的模型（即均值）和观测数据较小。

检查我们的假设

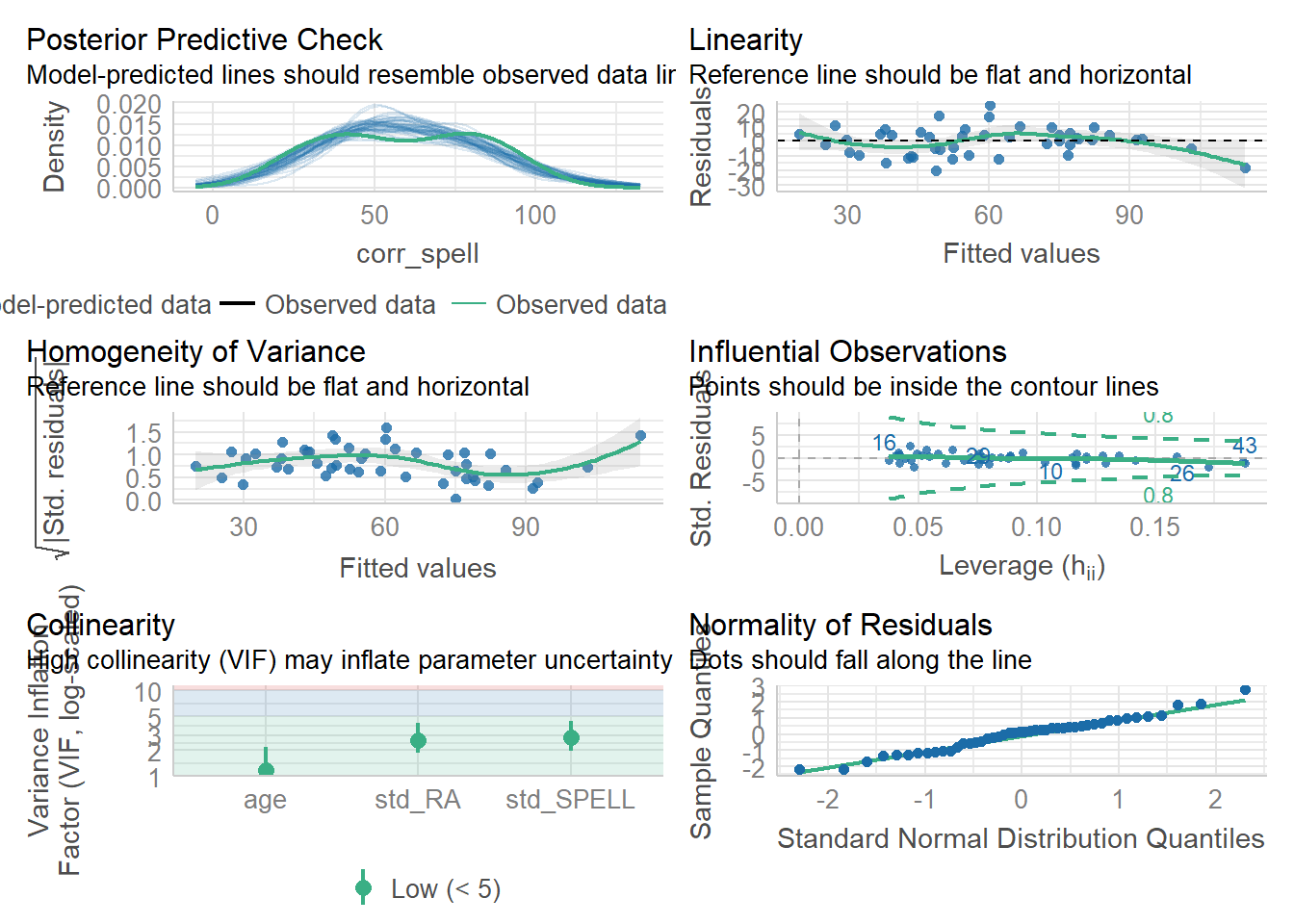
好的，所以它们是不同的 - 现在让我们来绘制关于我们模型假设的信息 - 记住，我们对我们的案例的Cook’s distance值特别感兴趣…

check_model(model1)

误差（errors）在我们拟合的值上分布相对均匀（同方差性） - 尽管对于高拟合值而言稍微糟糕一些 - 从 Q-Q 图中我们可以看出它们看起来相当正常（它们应该遵循对角线）。那么有关有影响力的案例呢？所以，第 10 个案例看起来有点可疑 - 它有一个较高的 Cook 距离值 - 这意味着它对我们的模型产生了不成比例的影响。让我们使用 filter() 函数将其排除 - 符号 != 表示“不等于”，因此我们选择除了第 10 个案例以外的值。

放弃一个有影响力的案例(Influential Case)

MRes_tut2_drop10 <- filter(MRes_tut2, case != "10")

重新建模数据

我们现在创建另一个模型（model2），不包括 Case 10。

model2 <- lm(corr_spell ~ age + RA + std_RA + std_SPELL, data = MRes_tut2_drop10)

让我们再次使用check_model()检查模型假设。

检查我们的假设

check_model(model2)

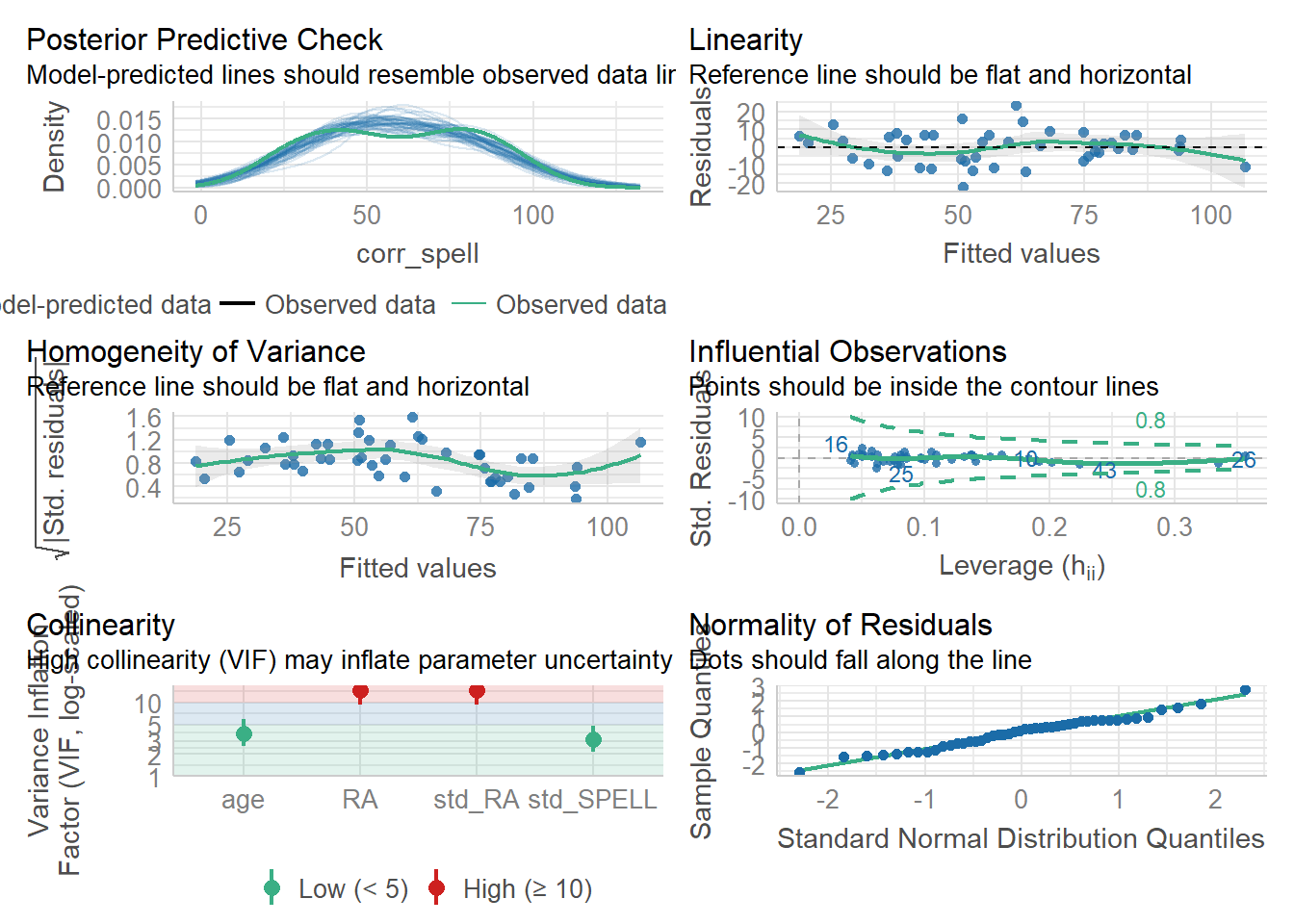
现在，让我们来看一下由VIF测量得出的多重共线性值：

vif(model2)

##       age        RA    std_RA std_SPELL 
##  3.843462 14.763168 14.672084  3.140457

看起来 RA 和 std_RA 有问题。我们可以使用 rcorr() 函数来研究它们之间的相关性：

rcorr(MRes_tut2_drop10$RA, MRes_tut2_drop10$std_RA)

##      x    y
## x 1.00 0.88
## y 0.88 1.00
## 
## n= 46 
## 
## 
## P
##   x  y 
## x     0
## y  0

重新建模数据

相关性很高（0.88），所以让我们排除具有最高VIF值的预测变量（即RA），并构建一个新模型：

model3 <- lm(corr_spell ~ age + std_RA + std_SPELL, data = MRes_tut2_drop10)
vif(model3)

##       age    std_RA std_SPELL 
##  1.190827  2.636186  2.821235

检查我们的假设

这些值现在看起来还不错。让我们再次检查模型假设。

check_model(model3)

总结模型

现在让我们生成系数（ coefficients），因为这看起来像一个合理的模型。

summary(model3)

## 
## Call:
## lm(formula = corr_spell ~ age + std_RA + std_SPELL, data = MRes_tut2_drop10)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.801  -6.907   1.327   5.155  24.669 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -209.4400    26.7210  -7.838 9.43e-10 ***
## age            1.1033     0.2133   5.172 6.09e-06 ***
## std_RA         0.3804     0.1385   2.747  0.00883 ** 
## std_SPELL      1.2107     0.1650   7.339 4.78e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.824 on 42 degrees of freedom
## Multiple R-squared:  0.8388, Adjusted R-squared:  0.8273 
## F-statistic: 72.87 on 3 and 42 DF,  p-value: < 2.2e-16

model0 <- lm(corr_spell ~ 1, data = MRes_tut2_drop10)
anova(model3, model0)

## Analysis of Variance Table
## 
## Model 1: corr_spell ~ age + std_RA + std_SPELL
## Model 2: corr_spell ~ 1
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1     42  4053.5                                  
## 2     45 25151.0 -3    -21098 72.866 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

我们将方程写成如下形式：

Spelled correct = -209.44 + 1.10(age) + 0.38(std_RA) + 1.21(std_SPELL) + residual

逐步回归

我们还可以进行逐步回归 - 向前是当您从空模型开始并添加预测变量，直到它们不能解释更多方差时，向后是当您从完整模型开始并删除预测变量，直到删除开始影响模型的预测能力。让我们保留案例 10 并删除高 VIF 预测变量 (RA)。这对于具有大量预测变量的模型非常方便，其中顺序回归的顺序不明显。

对数据进行建模

model0 <- lm(corr_spell ~ 1, data = MRes_tut2_drop10)
model1 <- lm(corr_spell ~ age + std_RA + std_SPELL, data = MRes_tut2_drop10)

让我们向前逐步回归：

steplimitsf <- step(model0, scope = list (lower = model0, upper = model1), direction = "forward")

## Start:  AIC=291.98
## corr_spell ~ 1
## 
##             Df Sum of Sq     RSS    AIC
## + std_SPELL  1   17802.2  7348.8 237.39
## + std_RA     1   14780.1 10370.9 253.23
## <none>                   25151.0 291.98
## + age        1      48.7 25102.3 293.89
## 
## Step:  AIC=237.39
## corr_spell ~ std_SPELL
## 
##          Df Sum of Sq    RSS    AIC
## + age     1   2567.20 4781.6 219.62
## + std_RA  1    714.14 6634.7 234.69
## <none>                7348.8 237.39
## 
## Step:  AIC=219.62
## corr_spell ~ std_SPELL + age
## 
##          Df Sum of Sq    RSS    AIC
## + std_RA  1     728.1 4053.5 214.02
## <none>                4781.6 219.62
## 
## Step:  AIC=214.02
## corr_spell ~ std_SPELL + age + std_RA

summary(steplimitsf)

## 
## Call:
## lm(formula = corr_spell ~ std_SPELL + age + std_RA, data = MRes_tut2_drop10)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.801  -6.907   1.327   5.155  24.669 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -209.4400    26.7210  -7.838 9.43e-10 ***
## std_SPELL      1.2107     0.1650   7.339 4.78e-09 ***
## age            1.1033     0.2133   5.172 6.09e-06 ***
## std_RA         0.3804     0.1385   2.747  0.00883 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.824 on 42 degrees of freedom
## Multiple R-squared:  0.8388, Adjusted R-squared:  0.8273 
## F-statistic: 72.87 on 3 and 42 DF,  p-value: < 2.2e-16

向后逐步回归：

steplimitsb <- step(model1, direction = "back")

## Start:  AIC=214.02
## corr_spell ~ age + std_RA + std_SPELL
## 
##             Df Sum of Sq    RSS    AIC
## <none>                   4053.5 214.02
## - std_RA     1     728.1 4781.6 219.62
## - age        1    2581.2 6634.7 234.69
## - std_SPELL  1    5198.3 9251.8 249.98

summary(steplimitsb)

## 
## Call:
## lm(formula = corr_spell ~ age + std_RA + std_SPELL, data = MRes_tut2_drop10)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.801  -6.907   1.327   5.155  24.669 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -209.4400    26.7210  -7.838 9.43e-10 ***
## age            1.1033     0.2133   5.172 6.09e-06 ***
## std_RA         0.3804     0.1385   2.747  0.00883 ** 
## std_SPELL      1.2107     0.1650   7.339 4.78e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.824 on 42 degrees of freedom
## Multiple R-squared:  0.8388, Adjusted R-squared:  0.8273 
## F-statistic: 72.87 on 3 and 42 DF,  p-value: < 2.2e-16

在逐步回归中使用向前和向后回归

steplimitsboth <- step(model0, scope = list (upper = model1), direction = "both")

## Start:  AIC=291.98
## corr_spell ~ 1
## 
##             Df Sum of Sq     RSS    AIC
## + std_SPELL  1   17802.2  7348.8 237.39
## + std_RA     1   14780.1 10370.9 253.23
## <none>                   25151.0 291.98
## + age        1      48.7 25102.3 293.89
## 
## Step:  AIC=237.39
## corr_spell ~ std_SPELL
## 
##             Df Sum of Sq     RSS    AIC
## + age        1    2567.2  4781.6 219.62
## + std_RA     1     714.1  6634.7 234.69
## <none>                    7348.8 237.39
## - std_SPELL  1   17802.2 25151.0 291.98
## 
## Step:  AIC=219.62
## corr_spell ~ std_SPELL + age
## 
##             Df Sum of Sq     RSS    AIC
## + std_RA     1     728.1  4053.5 214.02
## <none>                    4781.6 219.62
## - age        1    2567.2  7348.8 237.39
## - std_SPELL  1   20320.7 25102.3 293.89
## 
## Step:  AIC=214.02
## corr_spell ~ std_SPELL + age + std_RA
## 
##             Df Sum of Sq    RSS    AIC
## <none>                   4053.5 214.02
## - std_RA     1     728.1 4781.6 219.62
## - age        1    2581.2 6634.7 234.69
## - std_SPELL  1    5198.3 9251.8 249.98

检查我们的假设

check_model(steplimitsboth)

这些看起来不错。

summary(steplimitsboth)

## 
## Call:
## lm(formula = corr_spell ~ std_SPELL + age + std_RA, data = MRes_tut2_drop10)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.801  -6.907   1.327   5.155  24.669 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -209.4400    26.7210  -7.838 9.43e-10 ***
## std_SPELL      1.2107     0.1650   7.339 4.78e-09 ***
## age            1.1033     0.2133   5.172 6.09e-06 ***
## std_RA         0.3804     0.1385   2.747  0.00883 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.824 on 42 degrees of freedom
## Multiple R-squared:  0.8388, Adjusted R-squared:  0.8273 
## F-statistic: 72.87 on 3 and 42 DF,  p-value: < 2.2e-16

您会看到在每种情况下都会得到相同的最终模型。我们有三个重要的预测因子。

根据p值输入预测变量

我们还可以使用olsrr包中的ols_step_forward_p()函数 - 它的工作原理是根据p值输入预测变量来找到最佳模型。 olsrr包中还有其他方法。要查看它们，请在控制台窗口中输入olsrr:: 。

pmodel <- ols_step_forward_p(model1)
pmodel

## 
##                              Selection Summary                              
## ---------------------------------------------------------------------------
##         Variable                   Adj.                                        
## Step     Entered     R-Square    R-Square     C(p)        AIC        RMSE      
## ---------------------------------------------------------------------------
##    1    std_SPELL      0.7078      0.7012    34.1439    369.9304    12.9236    
##    2    age            0.8099      0.8010     9.5442    352.1614    10.5452    
##    3    std_RA         0.8388      0.8273     4.0000    346.5624     9.8241    
## ---------------------------------------------------------------------------

在这种情况下，具有最低 AIC 值的模型也是通过基于p值的顺序过程统计得出的模型 - 但情况可能并不总是如此。

帮助我们改进本节课程

线上自学课程问卷

线上工作坊问卷

Chapter 7 普通线性模型 - 回归 第二部分

概述

多元回归

我们需要的包

导入数据

检查可能的关系

对数据建模

检查我们的假设

放弃一个有影响力的案例(Influential Case)

重新建模数据

检查我们的假设

重新建模数据

检查我们的假设

总结模型

逐步回归

对数据进行建模

检查我们的假设

根据p值输入预测变量

帮助我们改进本节课程

Chapter 7 普通线性模型 - 回归第二部分